Các lũy thừa của bảng cửu chương
Ngày 23/01/2023 - 07:01Ở thời điểm đó các bảng tính được xây dựng bằng các thanh tre và có thể được sử dụng để nhân các số nguyên và một nửa lên đến 99,5. Một trong những ví dụ sớm nhất mà chúng tôi nhận ra là Bảng Pythagoras được Nichomachus đưa vào trong Giới thiệu về Số học của ông từ khoảng năm 100 sau Công nguyên.
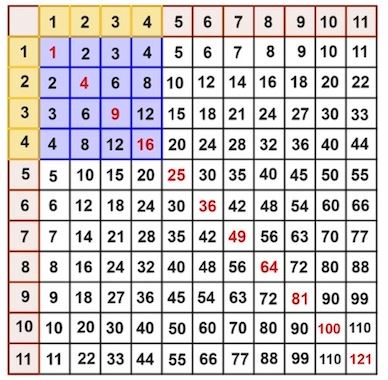
Ngày nay, ở trường, bảng cửu chương từ 1 đến 100 là một thiết bị mà học sinh sử dụng để học phép nhân thông qua việc luyện thuộc lòng và luyện trí nhớ nhanh. Mặc dù một số người coi việc thông thạo bảng nhân là một thành tựu, nhưng thực sự nó mang lại cho học sinh một nền tảng vững chắc để đặt viên gạch toán học. Hãy ngâm mình trong vùng nước sâu hơn và khám phá một số mẫu tuyệt vời tiết lộ sức mạnh ẩn chứa trong bảng cửu chương.
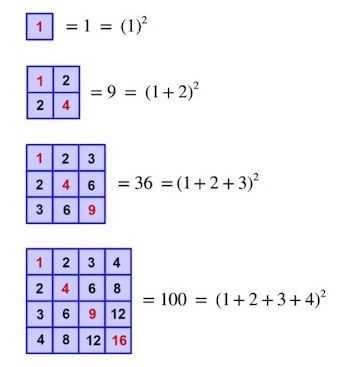
Hình tam giác và hình vuông
Trong một biển số nguyên, các số màu đỏ trên đường chéo chính (Tây Bắc đến Đông Nam) của bảng cửu chương rõ ràng là các số chính phương – các số đếm được nâng lên lũy thừa của 2.
Tính tổng các số trong mỗi mạng ô vuông bắt đầu từ hàng 1 và cột 1, cho chúng ta các số tam giác bình phương.
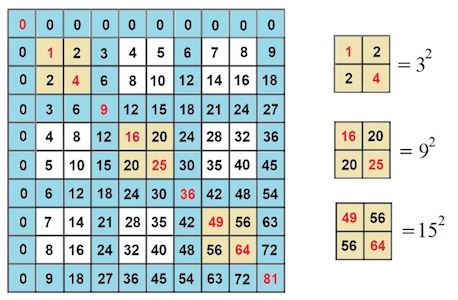
Các số tam giác không chỉ có thể được tìm thấy trong bảng cửu chương, nó còn có thể cho chúng ta các số bình phương, chúng ta đã thấy rằng khi các bội số của một số 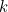 được tô màu xanh lam (xem bên dưới), tổng các số trong một mạng vuông được bao quanh bởi các bội số màu xanh lam này cũng bao gồm một số tam giác.
được tô màu xanh lam (xem bên dưới), tổng các số trong một mạng vuông được bao quanh bởi các bội số màu xanh lam này cũng bao gồm một số tam giác.
Tổng các số trong mạng hình vuông bằng (2m-1)(2n-1)T k bình phương -1 , trong đó m và n xác định mạng hình vuông bằng cách đếm lần lượt từ trên xuống và bên trái, và Tk-1 là k -1 số hình tam giác.
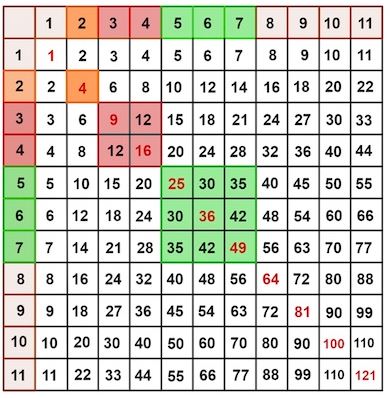
Chúng ta có thể thấy rằng tổng của các mạng vuông được bao quanh bởi các bội số màu xanh lam trên đường chéo chính (Tây Bắc đến Đông Nam) (được tô màu vàng bên dưới) cũng là các số chính phương. Điều này có thể dễ dàng được chứng minh bằng cách lấy công thức tổng ban đầu từ bài viết và sửa đổi nó. Chúng tôi sẽ chỉ sử dụng 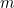 trong công thức vì vị trí dọc và ngang là như nhau.
trong công thức vì vị trí dọc và ngang là như nhau.
.png)
Chia ô vuông
Nếu chúng ta xem xét các dạng mạng vuông khác có kích thước và vị trí địa lý khác nhau trong bảng thời gian, chúng ta có thể tìm thấy nhiều số vuông hơn. Một mạng hình vuông xoay quanh đường chéo chính (Tây Bắc đến Đông Nam) dường như luôn tạo ra một số hình vuông tương ứng dựa trên tổng của các nhãn hàng và cột được chia sẻ.
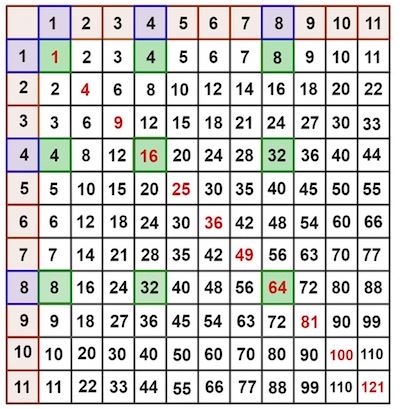
Điều này thậm chí dường như còn đúng khi một mạng vuông được xây dựng bằng cách giao nhau giữa các hàng và cột không liên tiếp. Nếu chúng ta lấy giao điểm của các hàng và cột 1, 4 và 8 , thì tổng của mạng hình vuông (được chia) là
Có một số hiểu biết toán học về lý do tại sao điều này hoạt động với ba số nguyên  và
và 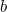 được
được  chọn từ bảng cửu chương để xác định mạng và chúng ta có thể đưa ra một công thức chung hoạt động cho ba số bất kỳ. Trong ví dụ của chúng tôi ở trên, tổng các số trong mạng vuông là:
chọn từ bảng cửu chương để xác định mạng và chúng ta có thể đưa ra một công thức chung hoạt động cho ba số bất kỳ. Trong ví dụ của chúng tôi ở trên, tổng các số trong mạng vuông là:















.jpg)





.jpg)

.jpg)

.jpg)
.png)


.png)










Bài viết liên quan
01/01/2023
06/01/2023
05/01/2023
02/01/2023
01/01/2023
01/01/2023